実行環境
OS : Windows 8.1 (64 bit)
Python : Python 3.2 (Scipy 0.14)
やりたいこと
陰関数(implicit function)を fitting したくなった。
陽関数(explicit function)なら最小二乗法(least square)を使えばいいんだがどうしたものか。
そもそも Igor や Origin と言った有名な解析ソフトはどうやってるのかぐぐってみた。
IGOR Pro/陰関数でフィッティング(Implicit Fitting)|ヒューリンクスのスタッフが書くブログサイトです。
http://blog.hulinks.co.jp/2011/04/ig-implicit-fitting.html
Nonlinear Implicit Curve Fitting (Pro Only)|OriginLab
http://www.originlab.com/doc/Origin-Help/Fitting-Implicit
ふむふむ、直交距離回帰 (Orthogonal Distance Regression, ODR) なる方法があるのね。
ODRPACK なるでかいライブラリがあるとのことでそこのマニュアルが詳しそう。
User’s Reference Guide for ODRPACK Version 2.01
Software for Weighted Orthogonal Distance Regression
http://docs.scipy.org/doc/external/odrpack_guide.pdf (pdf 直リン)
ODR は、fitting 曲線とのズレを考慮して、データ点から fitting 曲線までの距離*1の自乗和が最小になるパラメタを探すという方法ですかね。
頼りになる scipy にライブラリがあるらしく使ってみる。
Scipy.odr を使って楕円の式(陰関数)を fitting してみる
Scipy.odr のページ には陽関数のケースしか書いてない。
というわけでさっきの Igor のサイトのように楕円の式に対して fitting を行おうと思う。
具体的には長軸分の範囲に x を等間隔に配置した後に少しノイズをのせる。y も各 x に対しその値をノイズをのせて出力する。
あとはその (x, y) のデータに対し、ODR fitting を行う。
となる。
ここで若干の注意。基本的に
Orthogonal distance regression (scipy.odr) — SciPy v0.14.0 Reference Guide の通りなのだが、陰関数の場合、
- 関数を f(x,y) = 0 の形にしてその f を食わせる必要がある。
- Model のときの implicit を True にする。
- Data のときに y に 1 を与える必要がある。
さっきのスクリプトを動かして matplotlib で描いた結果がこれ。
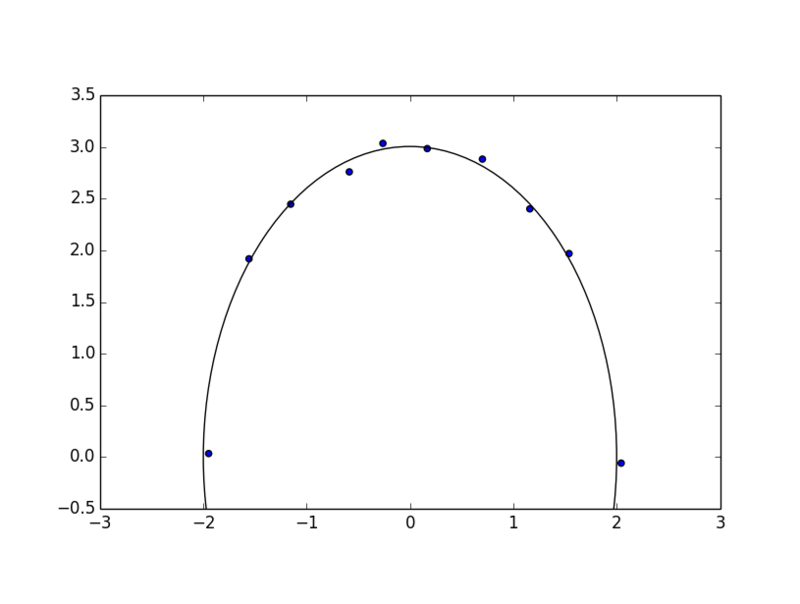
myoutput.pprint() による出力は
Beta: [ 2.00004406 3.00421792] Beta Std Error: [ 0.03151761 0.02818556] Beta Covariance: [[ 0.33647849 -0.09586991] [-0.09586991 0.26909395]] Residual Variance: 0.0029522237476154764 Inverse Condition #: 0.6735848530805985 Reason(s) for Halting: Parameter convergence
となった。ふむふむ、いい感じじゃないですかね。
参考にしたもの
Scipy.odr のメインページ。
楕円を描くときに用いた。こういったライブラリが充実してるのは非常にありがたい。
scipy.optimize.leastsq と scipy.odr の比較、検討とそれらの使用例を載せてあるサイト。非常に勉強になる。
感想、雑談
- scipy はやっぱすごかった!何を今更…。
- 非線形最小二乗法についてちゃんと勉強しておきたいなと感じた。線形の場合は正規方程式立てておりゃ~と線形計算するいう認識(あってるよね?)だったが、そう言えば非線形の場合の勉強してないな。
- Igor を研究室では使ってるので、それ使えよと言われそうなのですが生憎 Igor マクロ
覚える気がない書けないのです。scipy 使うメリットは高価なソフトがなくてもやりたい解析ができるというところですね。 - またしても matplotlib で苦戦したのでいい加減さらっと基本的なところを抑えておくべきか…。
- 周りの人に聞いてみたが、陰関数でのフィットはあまりしないようだ。ODR 以外にも有効な方法をご存知のかた、是非コメントにて教えて下さい!
*1:「曲線までの距離」を「曲線までの y 方向のズレ分」とするといつもの最小二乗法になる。
*2:これは scipy.odr.Data — SciPy v0.14.0 Reference Guide の Notes に "If y is an integer, then the Data instance can only be used to fit with implicit models where the dimensionality of the response is equal to the specified value of y." と記載がある。